Exponential And
Logistic Growth Model
The paper made use of two models to do prediction of the population growth of Tanzania. These include the Exponential Model and the Logistic Model.
Exponential Growth Model.
The exponential model is a mathematical model that describes the growth of a population over time. The model assumes that the population growth rate is constant. This means that the population will grow at a constant rate, regardless of its size and the available resources needed to accommodate this growth such as land, food, and many more.
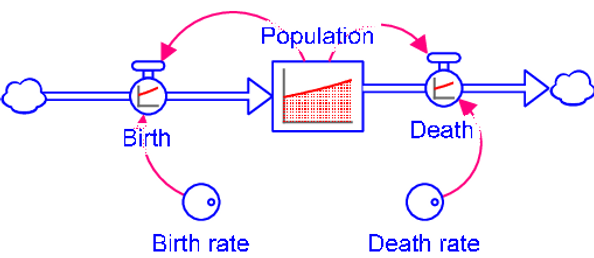
The logistic model is a mathematical model that describes the growth of a population over time. The model assumes that the population growth rate is not constant, but rather slows down as the population approaches its carrying capacity.
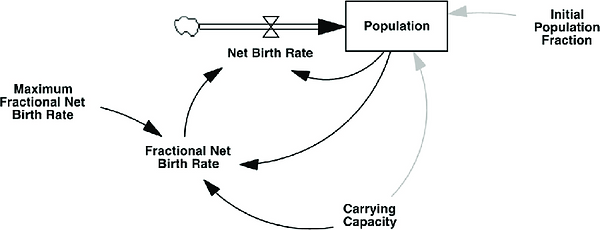
Logistic Growth Model.
Graphs of the two models:
Logistic Model
The logistic model can be represented by the following equation:
N(t) = K / (1 + A * e^(-at))
where:
-
N(t) is the population at time t
-
K is the carrying capacity which depends on several factors, including resources.
-
A is a constant that determines that depends on the carrying capacity and that of the initial population of Tanzania.
-
a is the growth rate of the population estimated at 2.88%
The logistic model can be derived from the following differential equation:
dN/dt = aN(K- N(t)/K)
where:
-
dN/dt is the rate of change of the population over time
-
K is the carrying capacity
Differential Equations for the Model
Exponential Model
The exponential Model is represented by:
N(t) = Noe^(at)
where:
-
N(t) is the population at any given time t
-
No is the initial population of Tanzania as of 1967 which was estimated at 12313467 people through census
-
a is the growth rate of the population using previous population data, estimated at 2.88%.
The exponential model was derived from the equation:
dN(t)/dt = aN(t)
where:
-
dN/dt is the rate of change of the population over time which could be solved using separation of variables to get the exponential model.
Model
Comparison of the models
-
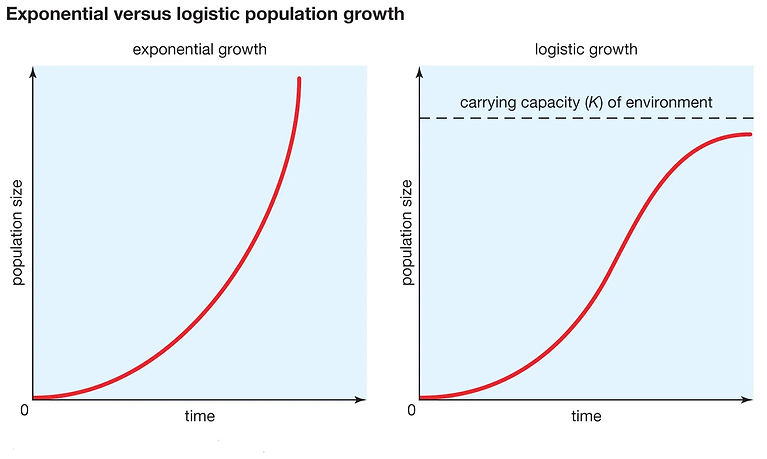
The exponential model and the logistic model are both mathematical models that can be used to project the population of Tanzania. However, the two models differ in their assumptions about population growth. The exponential model assumes that the population growth rate is constant, while the logistic model assumes that the population growth rate slows down as the population approaches its carrying capacity.
-
The exponential model is simpler to use than the logistic model, but it is also less accurate. The logistic model is more accurate than the exponential model, but it is also more complex to use.In the study, the exponential model was found to be slightly more accurate than the logistic model for both predicting the population of Tanzania from 1967 to 2012 and projecting the population of Tanzania from 2013 to 2035. However, the difference in accuracy between the two models was not statistically significant. The higher accuracy of the exponential model was counterintuitive to what we expected; but that could be because Tanzania's population is not close to its carrying capacity yet, which caused the logistic model that considers carrying capacity, to deviate a bit from the actual data.
Using the Model to Replicate the Figure
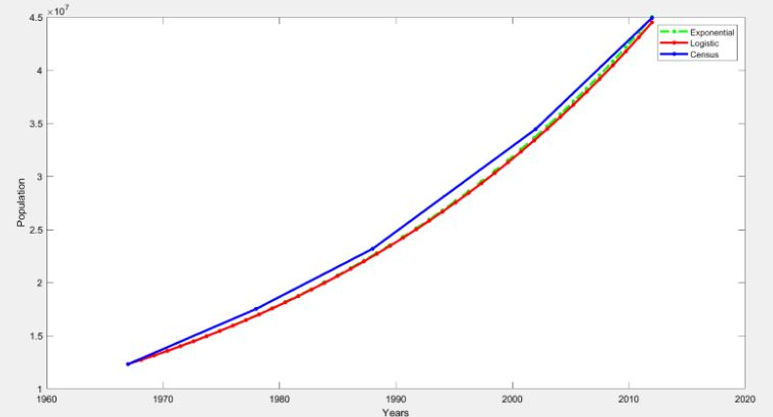
To make sure we really understood the models, our team decided to put them to the test. We used the models and data from the paper to recreate the first graph, which compares census data with exponential and logistic models from 1967 to 2012. Generally, we found a pretty close match between the models and the actual census data.
However, it's important to note that it wasn't a perfect match. The models didn't consider a lot of cases, and the fact that census data is collected over several years introduced some differences compared to the models.
Here's the comparison between our replicated figure and the one in the paper:

Figure from paper